写在前面

参考资料

• TI毫米波入门文档：The fundamentals of millimeter wave radar sensors
• 为什么在毫米波雷达中使用复基带信号：Using a complex-baseband architecture in FMCW radar systems
• 通信原理-角度调制I by 张锦皓Roger：通信原理 主讲：张锦皓

毫米波信号的表示

阅读很多论文，我发现非常多的文章都采用了复中频信号表示，例如载波频率为$f_c$，斜率为 $K$的毫米波雷达，距离为$R$的物体产生的回波信号可以表示为$s=exp(j4\pi(f_c+Kt)\frac{R}{c})$。当然，TI的毫米波雷达也确实是这么做的，原因可以参考TI的文章，大概可以概括为：复基带信号可以将FFT后的功率都变换到正频率边带上，方便处理、更加抗干扰。

但是这篇文章仍将使用传统的三角函数表示方式。只取实中频信号，无论如何仍旧是可行的，且更方便理解。如上面的回波信号，我们会写成$s=cos(4\pi(f_c+Kt)\frac{R}{c})$

复边带信号的虚部就是将实部向后推$\frac{\pi}{2}$个周期，我们可以很容易通过欧拉公式得到这个结论。

$s=exp(j4\pi(f_c+Kt)\frac{R}{c})=cos(4\pi(f_c+Kt)\frac{R}{c})+j\cdot sin(4\pi(f_c+Kt)\frac{R}{c})$

虚部的sin，可不就只与实部差1/4个周期吗？

（乘法）混频器的工作原理

之前阅读TI毫米波入门文档时，差频信号的产生依赖于发射（TX）信号与经过物体反射回到毫米波雷达的接收（RX）信号。假设发射信号和接收信号分别为$S_{TX}$与$S_{RX}$：

$S_{TX}=cos(2\pi f_0t+\varphi_0)$

$S_{RX}=cos(2\pi f_1t+\varphi_1)$

那么产生的差频信号就是：

$S_{IF}=cos(2\pi (f_0-f_1)t+(\varphi_0-\varphi_1))$

当时对于射频知识一无所知的我认为：混频器是一个超级高大上的器件，毫米波的频率有几十个GHz，怎么能做到实时处理如此高频的信号的？

当然，我现在已经知道，混频器，其实可以由一个乘法器+一个滤波器来进行实现。也就是将其两个输入的瞬时值直接相乘，再滤波，就能得到中频信号了。具体的数学推导也很简单，可以直接利用三角函数积化合差公式。

三角函数积化合差公式（之一）:

$cos(a)+cos(b)=\frac{1}{2}\cdot (cos(a+b)+cos(a-b))$

因此：

$S_{TX}\cdot S_{RX}= cos(2\pi f_0t+\varphi_0)cos(2\pi f_1t+\varphi_1)=...$

$...=\frac{1}{2}\cdot (cos(2\pi (f_0+f_1)t+(\varphi_0+\varphi_1))+cos(2\pi (f_0-f_1)t+(\varphi_0-\varphi_1)))$

我们可以看到，我们需要的中频信号已经得到了。只需将乘法器的结果通过一个低通滤波器，将频率成分$f_0+f_1$滤掉，保留$f_0-f_1$就行了。

在TI文档上展示的混频器如下图中的mixer所示：

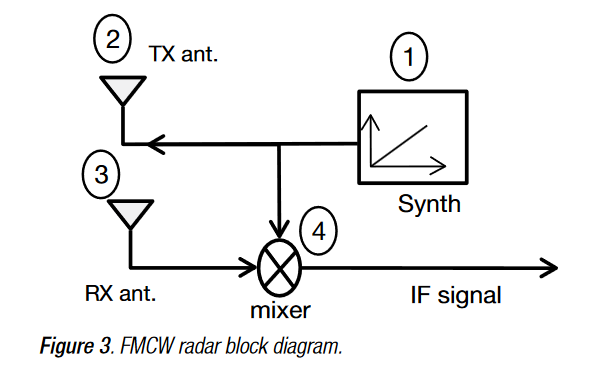
FMCW雷达中频信号的推导

调幅与调角

假设载波信号的表达式为：$S_c=Acos(\omega_ct+\varphi)$

通过改变载波信号幅度的调制方式，称作调幅：$S_{AM}=A(t)cos(w_ct+\varphi)$

通过改变相位的调制方式，称为调角：$S_{Angle}=Acos(\omega_ct+\varphi(t))$

调频与调相，都是调角的一种。

瞬时相位与瞬时角频率

所谓“瞬时”，指的是特定的$t$时刻，载波信号的状态。

瞬时相位就是把cos表达式括号内的表达式直接拿出来。例如：$S_c=Acos(\omega_ct+\varphi)$的瞬时相位就是$\omega_ct+\varphi$。瞬时相位就是信号已经经过的周期数乘以$2\pi$。

瞬时角频率（也许可以叫瞬时角速度）就是瞬时相位对时间的导数。在调频的情况下：$\varphi$不是时间的函数，则瞬时角频率等于载波频率$\omega_c$；在调角的情况下，$\varphi(t)$是时间的函数，则瞬时角频率等于载波频率$\omega_c$加上调角带来的瞬时角频偏$\frac{d\varphi}{dt}$。

可以将信号看作一个圆周运动物体的轨迹，$\omega$是角速度，$\varphi$是初始位置与0角度参考线（极坐标中的极轴）的夹角。瞬时相位就是物体的当前位置，而瞬时角频率则是瞬时角速度。

调相与调频

调相与调频都属于调角，区别在于基带信号$m(t)$与瞬时相位差$\varphi(t)$之间的关系。

调相信号的瞬时相位差与基带信号具有正比例关系，即$\varphi(t)=K_pm(t)$，其中常数$K_p$称为相移常数。调相信号的表达式为：$S_{PM}=Acos(\omega_ct+K_pm(t))$

调频信号的瞬时角频偏与基带信号具有正比例关系，即$\frac{d\varphi}{dt}=K_fm(t)$，其中常数$K_f$称为频偏常数。调相信号的表达式为：$S_{FM}=Acos(\omega_ct+K_f\int m(\tau)d\tau)$

FMCW雷达的载波

FMCW雷达采用调频技术，频率随时间线性变化。这里的频率可以认为是瞬时角频率。$\frac{d(\omega_c t +\varphi)}{dt}=\omega_c + \frac{d\varphi}{dt}$

由于载波频率$\omega_c$是常数（在TI的设备上一般是60GHz或77GHz），因此：$\frac{d\varphi}{dt}$随时间线性变化。假设FMCW雷达的频率（角速度）对时间的斜率为$K$，即：$\frac{d\varphi}{dt}=Kt$。

记$\varphi'(t)=\frac{d\varphi}{dt}=Kt$我们就可以利用积分算出瞬时相位：$\varphi(t)=\int \varphi'(\tau)d\tau=\int K\tau d\tau=\frac{K}{2}t^2+c$

因此，我们可以得到FMCW载波的最终表达式：$S_{FMCW}(t)=Acos(\omega_c t+\frac{K}{2}t^2+c)$。

我们已经知道了瞬时频率与时间的变化关系是线性的，我们当然可以认为载波频率$\omega_c$是一个随时间变化的量$\omega_c(t)=\omega_c(0)+Kt$，这样一来FMCW载波的表达式就变为$S_{FMCW}(t)=Acos((\omega_c +Kt) t+c)$。这也能得到只差一个系数$\frac{1}{2}$的正确结果。

但是，当我们想要把一个任意的基带信号$m(t)$以调频方式加载到载波上时，我们不能简单地直接把基带信号加在载波频率上，例如：$Acos((\omega_c+km(t))t)$。这样求出的瞬时频偏不会等于$km(t)$，会得到不正确的结果。

中频信号的推导

调频连续波信号的返回信号是发射信号的延时信号。延时时间$t_0=\frac{2d}{c}$，$d$为反射物与雷达的距离。因此：

发射信号：$S_{TX}(t)=Acos(\omega_c t+\frac{K}{2}t^2+c)$

接收信号：$S_{RX}(t)=Acos(\omega_c (t-t_0)+\frac{K}{2}(t-t_0)^2+c)$

中频信号是二者的混频，由前面得到的积化和差公式，加上低通滤波可得：

$S_{IF}(t)=Acos(Kt_0t+\omega_ct_0-\frac{K}{2}t_0^2)$

由于$t_0$非常小，因此可以忽略关于$t_0^2$的高阶小量，中频信号的最终表达式为：

$S_{IF}(t)\approx Acos(Kt_0t+\omega_ct_0)$

与TI文档给出的中频信号表达式相比：

其中，$Kt_0=2\pi S\frac{2d}{c}=2\pi f_o$，$\omega_ct_0=2\pi f_c\frac{2d}{c}$。由于波速除以频率等于波长，即$\lambda=\frac{c}{f_c}$，故$\omega_ct_0=\frac{4\pi d}{\lambda}$。完全一致，推导完成！